Entropy and Self Information

This post contains short notes on entropy and self information and why machine learning adopted them from information theory.

Information theory is a science concerned with the study of quantification of information.

Self information

In order to deal with information from a quantitive and not qualitative perspective, Claude Shannon invented a formula to quantify how much information is contained inside an event.

The breakthrough idea of Shannon follows from the intuition that the more unlikely an event is, the higher its information - and vice versa.

Assuming a set of possible events \(X = {x_0, x_1, ... x_n}\) with a corresponding probability distribution such that each \(x_i\) has a probability of \(p(x_i)\), we want to derive a quantity, which we shall define information content of \(x_i\) or \(h(x_i)\) such that the higher \(p(x_i)\) the lower \(h(x_i)\). We define

\[h(x_i) = log(\frac{1}{p(x_i)}) = -log(p(x_i))\]

to be the self information of event \(x_i\).

As we know, the number of bits to represent a number \(N\) is \(log_2(N)\). Therefore, we can look at the self information as the number of bits necessary to represent (store, transmit) the probability of an event.

Entropy

Entropy in information theory (as it also exists in other fields, such as thermodynamics) is the natural extension of the concept of self-information to random variables. Entropy tells us how much information we find on average in a random variable \(X\).

Assuming we have a random variable \(X\), we define the Entropy of \(X, H(X)\) as:

\[\sum_i p(x_i) h(x_i) = - \sum_i p(x_i) log(p(x_i))\]

Entropy is the average number of bits needed to represent the probability of an event from the random variable \(X\).

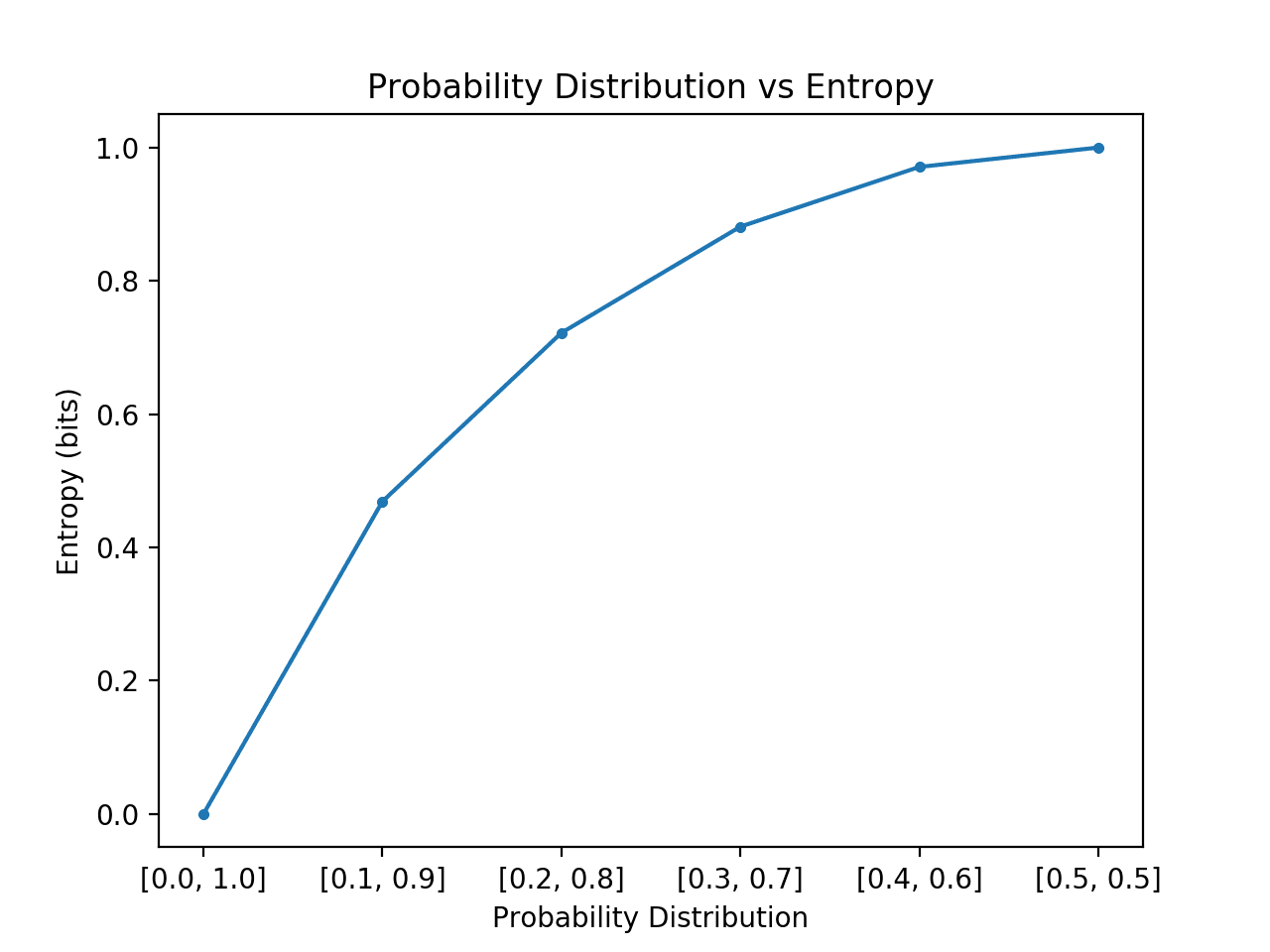
The more a probability distribution is balanced, that is, all events are similarly likely, the higher is the entropy. The more unbalanced the distribution, the lower the entropy. Look at the chart from [1] that plots entropy for a probability distribution with only two events.

Cross entropy

Cross entropy is a popular metric in machine learning, used to measure the difference between two probability distributions.

The intuition for this definition comes if we consider a target or underlying probability distribution \(P\) and an approximation of the target distribution Q, then the cross-entropy of \(Q\) from \(P\) is the number of additional bits to represent an event using \(Q\) instead of \(P\). More precisely, in classification problems, the predicted probabilities \(Q\) (output of a model) can be compared with the true probabilities \(Q\) (one-hot encoded ground truth labels).

Reference

1. https://machinelearningmastery.com/what-is-information-entropy/
2. http://colah.github.io/posts/2015-09-Visual-Information/
3. C. Bishop, Pattern Recognition and Machine Learning