LogitLens From Scratch With Hugging Face Transformers
In this short tutorial, we’ll implement LogitLens to inspect the inner representations of a pre-trained Phi-1.5. LogitLens is a straightforward yet effective interpretability method.
The core idea behind it is to apply the language model’s output layer (also known as the “unembedding matrix” or “language modeling head”) to the hidden states at each layer of the transformer. This allows us to see how the model’s internal representations change as the input progresses through the network. Surprisingly, the model often acquires a significant amount of semantic understanding in the earlier layers of the transformer. By inspecting the predicted tokens at each layer, we can observe how the model’s understanding of the input evolves.
Disclaimer: ✋ If you’re looking for advanced interpretability tools, there are plenty of powerful libraries out there. But here, we’re going back to basics and do this from scratch because it’s always cool to understand how things work under the hood.
We’ll use Microsoft Phi-1.5 here since it’s a small, open model. Feel free to swap in another Hugging Face model.
from transformers import AutoModelForCausalLM, AutoTokenizer
import torch
model_id= "microsoft/phi-1.5"
# load the model
model = AutoModelForCausalLM.from_pretrained(model_id, torch_dtype=torch.bfloat16).eval().to(device)
tokenizer = AutoTokenizer.from_pretrained(model_id, add_bos_token=True, bos_token='<bos>', use_fast=False)
Downloading the model might take a while, so you better pick a small model :). Let’s now consider an example input sentence and tokenize it.
example = "The quick brown fox jumps over the lazy"
inputs = tokenizer(example, return_tensors="pt").to(device)
print("Input shape: ", inputs["input_ids"].shape)
Input shape: torch.Size([1, 9])
The sentence was encoded into 9 tokens. In case you want to know what the tokens looks like, you can just decode them back:
original_input_tokens = tokenizer.convert_ids_to_tokens(inputs["input_ids"][0], skip_special_tokens=False)
print("Input tokens: ", original_input_tokens)
Input tokens: ['<bos>', 'The', 'Ġquick', 'Ġbrown', 'Ġfox', 'Ġjumps', 'Ġover', 'Ġthe', 'Ġlazy']
As we can see, the tokenizer added the beggining of sentence <bos> token. The ugly Ġ represent spaces.
In the notebook you can find a function clean these up a bit (I find the Ġs are really annoying):
original_input_tokens = cleanup_tokens(original_input_tokens)
original_input_tokens
['<bos>', 'The', ' quick', ' brown', ' fox', ' jumps', ' over', ' the', ' lazy']
Now, let’s feed the input into the model to get the next token prediction along with all the hidden states. Fortunately, the model’s forward method provides an option to return its hidden states.
# we need all the intermediate hidden states
with torch.no_grad():
outputs = model(**inputs, output_hidden_states=True)
# # print(outputs.keys())
print("Logits shape: ", outputs["logits"].shape)
Logits shape: torch.Size([1, 9, 51200]) # (batch, sequence len, vocab size)
The logits have been already projected into the vocabulary space. Hidden states on the other hand are still “raw” token representations. We’ll have one hiddent state vector for each model layer.
hidden_states = outputs.hidden_states
print("Number of model layers", len(hidden_states))
print("Hidden states for first layer", hidden_states[0].shape)
Number of model layers: 25
Hidden states for first layer: torch.Size([1, 9, 2048])
As we see, each layer in the model produces a hidden state. Here the last dimension represents the embedding size (not the vocbulary size).
By applying the language modeling head (or unembedding matrix) to the hidden state at any layer, we can generate ‘early’ logits—predictions from intermediate representations. While the model isn’t explicitly trained to produce meaningful logits at these layers, we’ll see that it naturally starts embedding token-level information along the way.
We can apply the language modeling head like this:
logits_at_second_layer = model.lm_head(hidden_states[2])
print("Logits at second layer shape: ", logits_at_second_layer.shape)
Logits at second layer shape: torch.Size([1, 9, 51200])
We now want to access the hidden state at each layer, apply the language modeling head to get the logits, and finally decode the logits into tokens.
for i, hidden_state in enumerate(hidden_states):
# apply the language model head to the hidden states
logits = model.lm_head(hidden_state)
# decode the logits to get the predicted token ids
predicted_token_ids = logits.argmax(-1)
# convert the token ids to tokens
predicted_tokens = tokenizer.convert_ids_to_tokens(predicted_token_ids[0], skip_special_tokens=False)
predicted_tokens = cleanup_tokens(predicted_tokens)
# append the predicted tokens to the list for later
logitlens.append(predicted_tokens)
print(f"Layer {i}: {predicted_tokens}")
Layer 0: ['-', ' S', '-', '-', '-', '-', '-', ' S', '-']
Layer 1: ['ed', 'oret', 'est', 'ies', 'es', 'uit', ' the', ' same', ' double']
Layer 2: ['import', 'oret', 'est', 'ies', 'es', 'uits', ' time', ' same', ' part']
Layer 3: ['import', 'orem', 'est', 'arf', 'es', 'es', ' all', ' entire', ' man']
Layer 4: [' realise', 'orem', 'est', 'arf', 'es', 'uit', 'worked', ' entire', ' man']
Layer 5: [' realise', 'orem', 'est', 'arf', 'es', 'uit', 'worked', ' entire', ' man']
Layer 6: [' realise', 'orem', 'est', 'arf', 'es', 'uit', 'kill', 'ses', ' man']
Layer 7: ['iveness', 'orem', 'est', ' fox', 'es', 'ers', ' all', ' entire', ' brown']
Layer 8: ['iveness', 'orem', 'ness', ' fox', 'es', 'ers', 'ind', ' entire', ' poor']
Layer 9: ['iveness', 'orem', 'ness', ' fox', 'es', 'ers', ' obstacles', ' entire', ' poor']
Layer 10: ['iveness', 'orem', 'ness', ' ph', 'es', 'ers', ' obstacles', ' entire', ' poor']
Layer 11: ['iveness', 'orem', ' brown', ' fox', 'es', 'ers', ' obstacles', ' entire', ' poor']
Layer 12: ['iveness', 'oret', ' brown', ' fox', 'es', ' into', ' obstacles', ' entire', ' poor']
Layer 13: ['ality', 'oret', ' brown', ' fox', 'es', ' into', ' obstacles', ' entire', ' poor']
Layer 14: ['ality', 'ory', ' brown', ' ph', 'es', ' into', ' obstacles', ' entire', ' poor']
Layer 15: ['iveness', 'ory', ' brown', ' fox', 'es', ' into', ' obstacles', ' entire', ' poor']
Layer 16: ['import', 'ory', ' brown', ' fox', 'es', ' into', ' lazy', ' entire', ' poor']
Layer 17: ['import', 'mes', ' brown', ' fox', 'es', ' over', ' the', ' lazy', ' poor']
Layer 18: ['import', ' first', ' brown', ' fox', 'es', ' over', ' the', ' lazy', ' dog']
Layer 19: [' example', ' first', ' brown', 'Ċ', 'es', ' over', ' the', ' lazy', ' dog']
Layer 20: ['ĊĊ', ' first', ' brown', 's', 'es', ' over', ' the', ' lazy', ' dog']
Layer 21: ['ing', ' first', ' brown', ' fox', 'es', ' over', ' the', ' lazy', ' dog']
Layer 22: ['Ċ', ' first', ' brown', 'Ċ', ' jumps', ' over', ' the', ' lazy', ' dog']
Layer 23: ['Ċ', 'Ċ', ' brown', ' fox', ' J', ' over', ' the', ' lazy', ' dog']
Layer 24: ['Ċ', 'ory', ' brown', ' fox', ' jumps', ' over', ' the', ' lazy', ' dog']
As you observe, the predictions refine layer-by-layer, reflecting the model’s gradual understanding of the input. We can visualize the predictions with a heatmap:
# create a heatmap that has a row for each list in the logitlens list
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
sns.set_theme(style="white")
# just for the bkg color
intensities = np.ones((len(hidden_states), len(original_input_tokens)))
# Create heatmap
plt.figure(figsize=(20, 10))
ax = sns.heatmap(intensities[::2],
annot=cleanup_tokens(logitlens)[::2],
fmt='',
cmap='Greys',
xticklabels=original_input_tokens,
yticklabels=list(range(len(logitlens)))[::2],
cbar=False
).invert_yaxis()
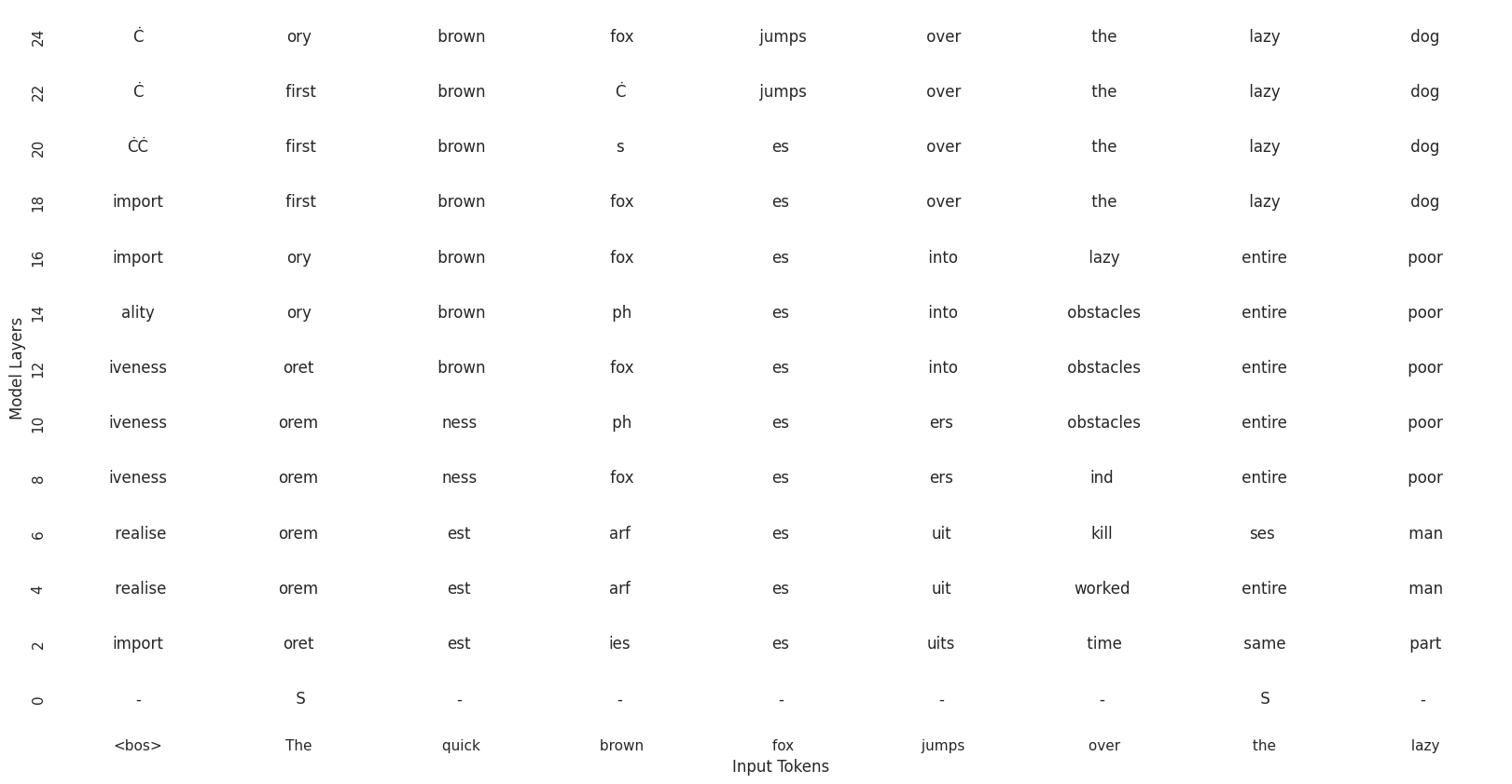
Right now, our heatmap just displays the model’s top predictions (using argmax), which is fine but a bit flat. Let’s make it more interesting by incorporating model certainty into the visualization.
A good way to quantify the model’s certainity about its output is looking at the entropy of the output distribution. Let’s replace the background color of each cell with the entropy of the model when generating that token.
We’ll calculate the entropy of the output distribution, using it to color the background:
# aux function to compute the entropy from logits
def entropy_from_logits(logits):
probs = torch.nn.functional.softmax(logits, dim=-1).clamp(1e-8, 1) #avoid nans
return -torch.sum(probs * torch.log(probs), dim=-1).squeeze()
Now we can run the same code as before, this time we’ll also compute and store the entropies.
logitlens = []
entropies = []
for i, hidden_state in enumerate(hidden_states):
# apply the language model head to the hidden states
logits = model.lm_head(hidden_state)
# get the entropy of the logits
entropy = entropy_from_logits(logits).float().cpu().detach().numpy()
# decode the logits to get the predicted token ids
predicted_token_ids = logits.argmax(-1)
# convert the token ids to tokens
predicted_tokens = tokenizer.convert_ids_to_tokens(predicted_token_ids[0], skip_special_tokens=False)
predicted_tokens = cleanup_tokens(predicted_tokens)
# append the predicted tokens to the list
logitlens.append(predicted_tokens)
entropies.append(entropy)
print(f"Layer {i}: {predicted_tokens}")
Let’s now create a plot where each cell is colored based on the entropy.
# Create figure and axis
plt.figure(figsize=(20, 10))
# Create heatmap
ax = sns.heatmap(np.stack(entropies)[::2],
annot=logitlens[::2],
fmt='',
cmap='YlGnBu',
xticklabels=original_input_tokens,
yticklabels=list(range(len(logitlens)))[::2],
).invert_yaxis()
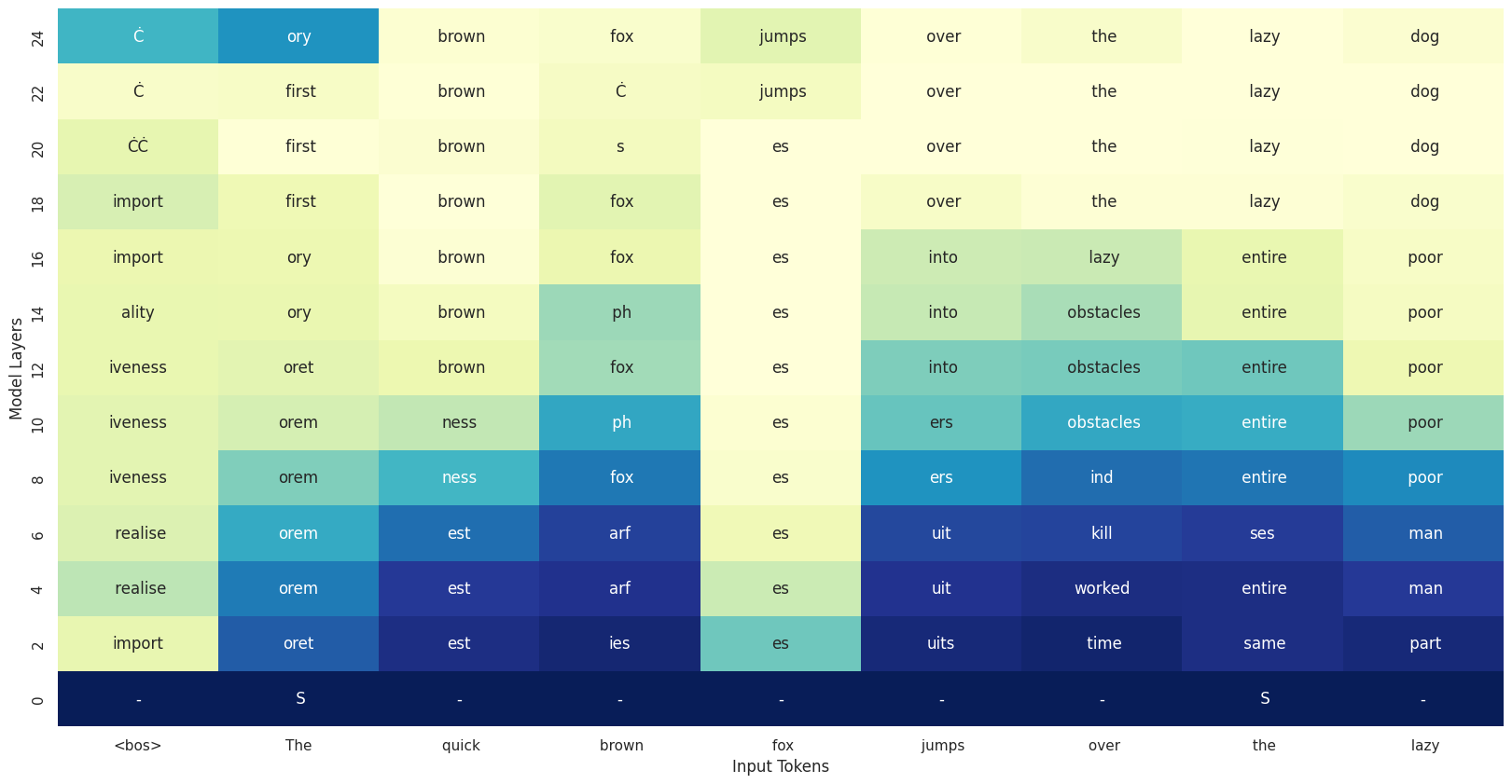
Final consideration
I recently came across a nice blog by Sonia Joseph, pointing out that the logit lens is a convenient way to investigate internal representations. But it can be misleading, as it depends on the layer’s basis vector alignment with the output space. Linear probes often show that decent representations can be present in much earlier layers than what the logit lens portrays.
Hope you liked this! If you have any suggestions/questios, feel free to drop me a message/email or visit my page or my twitter @devoto_alessio.
Thanks Luigi for reviewing this!
